Recently I’ve been spending some time in the evening playing around with Rust. My go-to project for learning systems-y languages has always been chess engines. If there is one thing to say about building chess engine it’s don’t do it — it becomes an addiction, and it’s never finished.

One of the foundations for a decent chess engine is a reasonably fast move generation function. This is a method that takes a chess position, and returns a list of all the moves that can be made from that position for a given side.

For example: At the starting position there are 20 moves for white: each of the pawns can move forward one or two spaces (16 moves total), and the knights have two moves each (4 moves total).

In this article I’ll talk about how to generate moves for a chess position efficiently, as well as some common ‘gotchas’ that can lead to bugs.

There are two approaches to generating moves in a chess engine, dubbed “legal” and “psuedo-legal”

Pseudo-legal move generation

This is the simplest way of generating moves. A pseudo-legal move generator does not consider checks or pins when generating moves. It simply looks at the board and sees what squares are empty (pushes) or have enemy pieces on (captures).

For example, in the following position, a pseudo-legal move generator would generate the move for black king to f8, even though it puts the king in check from white’s rook.

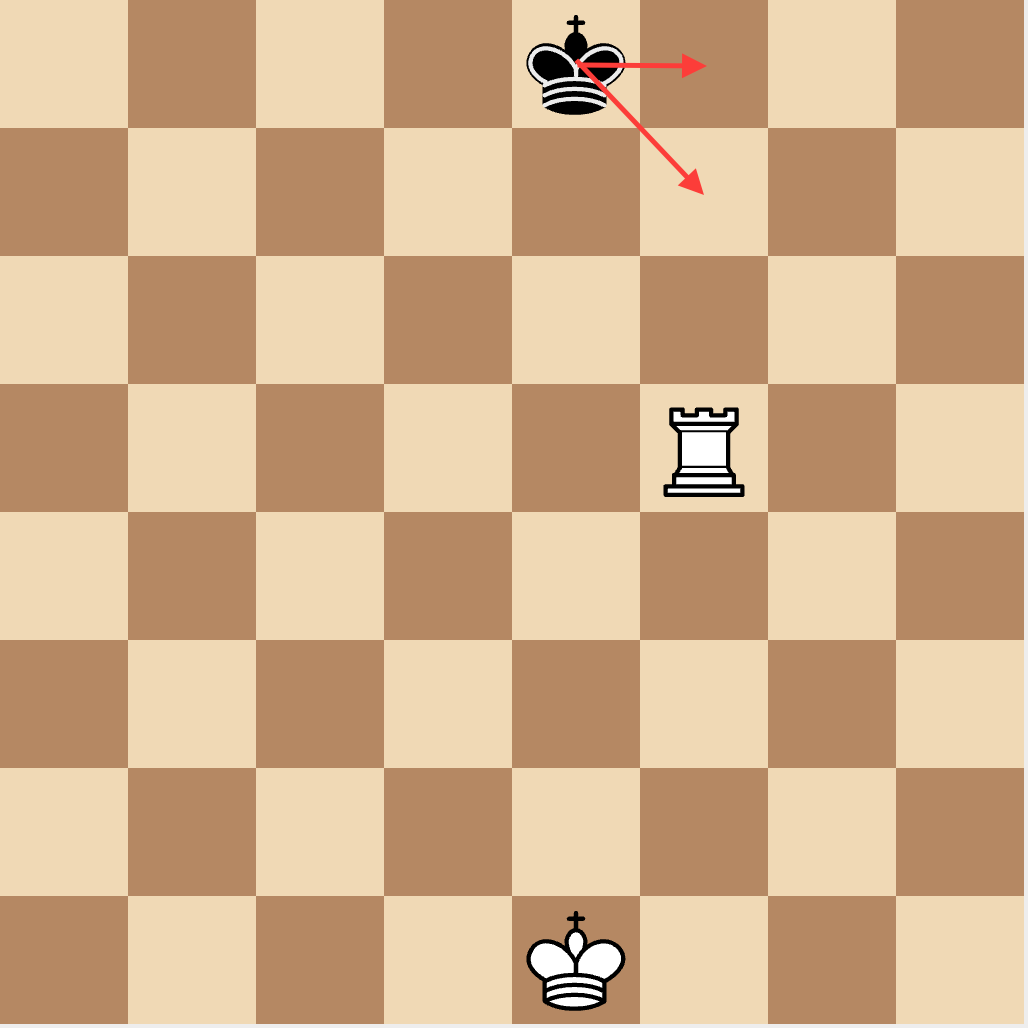
When using a psuedo-legal move generator you have to check that the board is still valid after making a move, and then void the move if it was invalid — like moving the king into check in the move above.

Generating pseudo-legal moves is a lot faster than just generating legal moves because calculating checks and pins is hard. However in chess it’s only legal moves that we care about, so you still have to test your moves for legality after making them, and then undo the move if it turned out to be invalid. It turns out that this is less efficient because making and unmaking a move takes time — it’s quicker to simply not generate bad moves in the first place.

Legal move generation

Here are the steps required to generate legal moves:

Part 1: King moves

In chess you cannot move your king to any squares attacked by the opponent’s pieces, i.e. you can’t move into check. So to generate valid king moves we first need to work out what squares are attacked by the opponent. To do this efficiently we can use bit-boards to represent the attacked squares. This is a 64-bit integer representing the squares on a chess board. A ‘1’ or set bit means the square is attacked, and a ‘0’ or unset bit means it isn’t. Using the position above, the bit-board of squares attacked by white will look like this (with set bits denoted by red X’s):

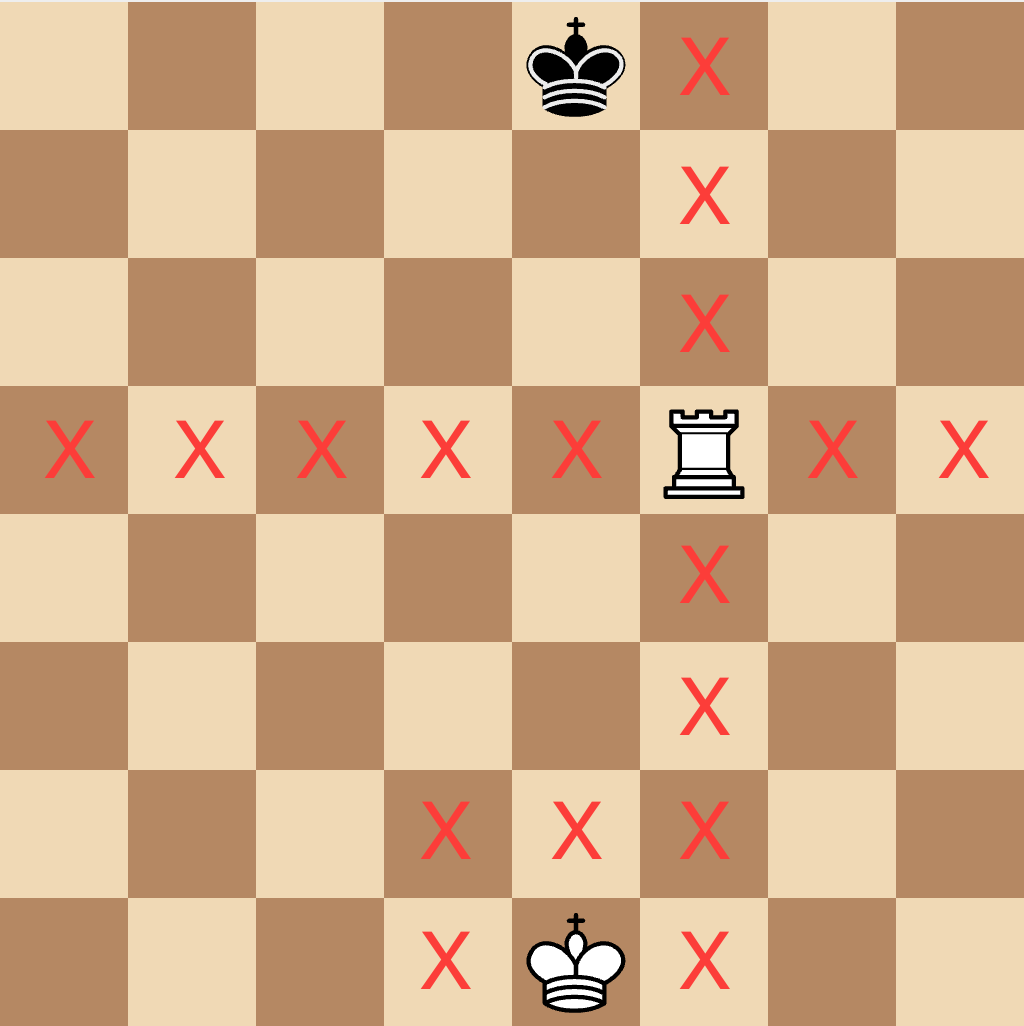
We can calculate valid king moves by ensuring that we never move to a square that is attacked.

Gotcha: King moves away from a checking slider

There is the following catch when generating king moves. Suppose it’s black’s turn to move and we have this position (white attacks are represented by red X’s):

Here valid king moves for black are d7, d8, f7 and f8 to get away from white’s rook. However e8 (the question mark), though invalid, also moves the king out of the set of squares attacked by white’s rook!

This exposes an issue with the way we’re generating our attacking squares. Because the king blocks the white rook’s attack, it looks as though the white rook isn’t attacking e8 — but we know this is not a valid move for black’s king. The solution is to remove the black king from the board when calculating the bit-board of squares attacked by white:

This way the rook “sees through” black’s king and our set of squares the king must avoid is correct. In my engine I call this bit-board king danger squares to avoid confusion with the subtly different attacked squares bit-board. By filtering out any king moves to king danger squares we can ensure that only legal king moves are generated.

Part 2: Check evasions

If we’re in check, the number of moves we can make is very restricted. To calculate whether we’re in check, you can look at moves from the king square by each kind of piece.

For example to find out whether black is in check in the following position:

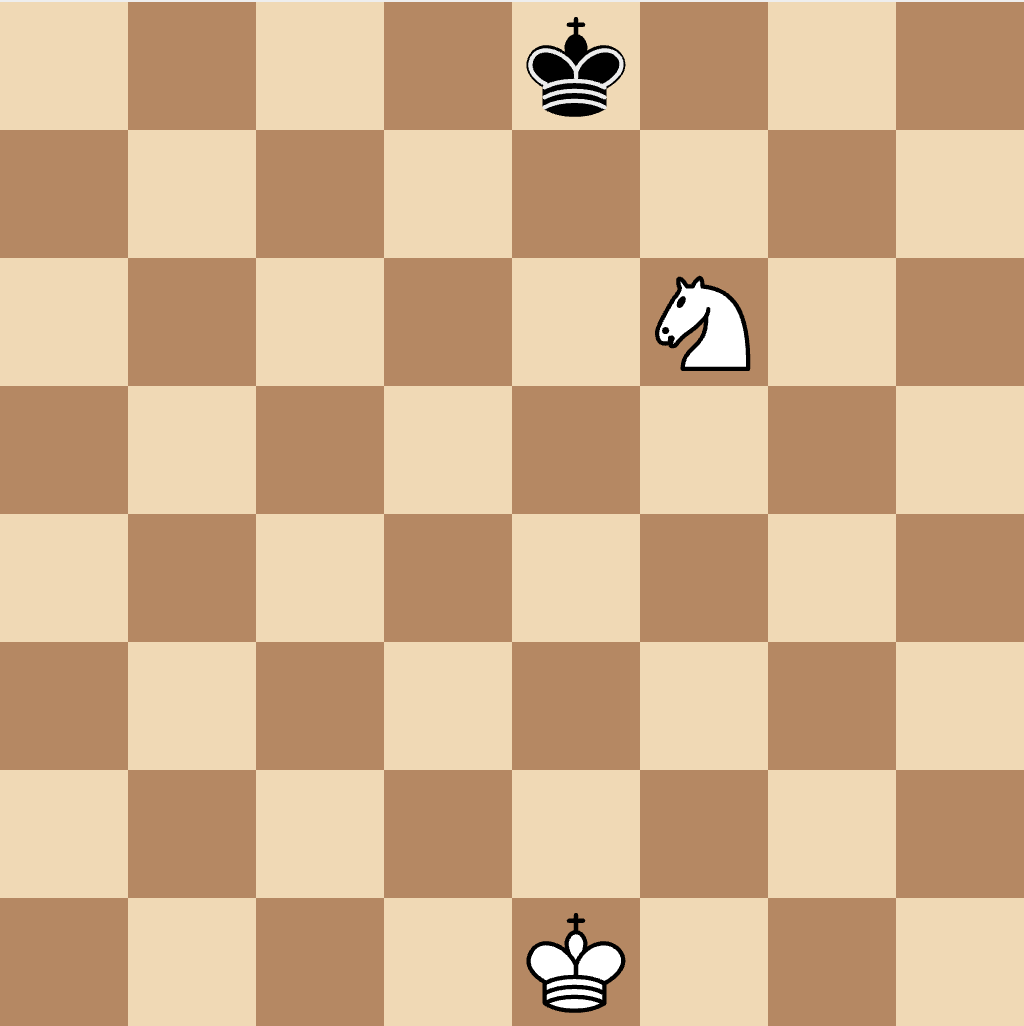
Pretend there is a white knight on the king square on e8, then see if any moves from this square land on actual white knights. In my rust code it looks something like this:

let mut attackers = Bitboard(0); // empty bitboard
attackers |= KNIGHT_MOVES[king_sqare] & opponent_knights;

By repeating this for each enemy piece type you can build a bit-board of pieces giving check. If it’s not empty, you’re in check. You can ignore opponent king moves here because it’s impossible for a king to give check to another king.

Double check

If there is more than one enemy piece attacking the king, we’re in double check. Here’s an example:

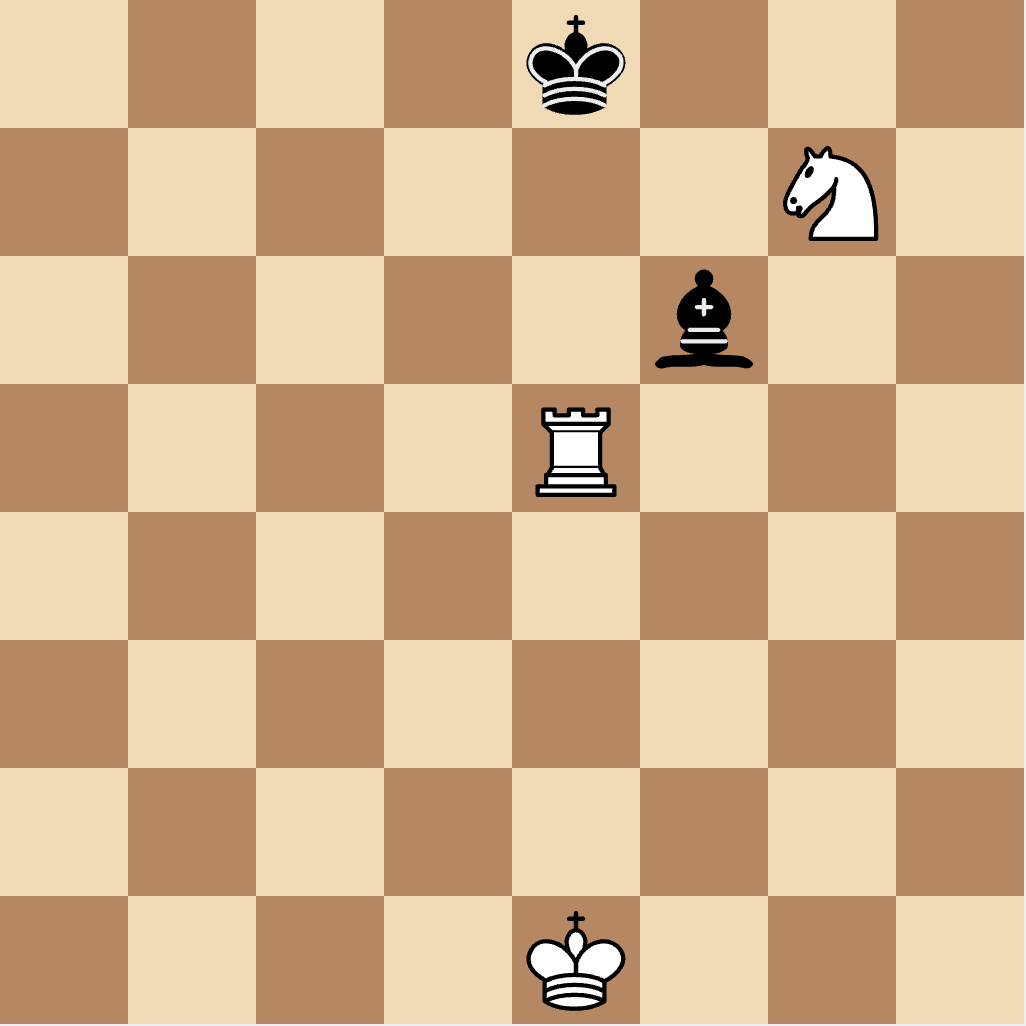
Here black is in check from white’s rook on e5 and white’s knight on g7. Since black is in check from two pieces, black’s bishop on f6 can’t help out as black will still be in check no matter which white piece is captured. Therefore when in double check the only legal moves are king moves.

Assuming we’ve already generated all the king moves at this point, we can exit early if there is more than one attacker:

let num_checkers = attackers.pop_count();

if num_checkers > 1 {
  return // only king moves valid if double check
}

Single check

Most checks will be “single-checks”, i.e. only one piece is checking the king. In this case there are three things we can do:

Move the king out of check
Capture the checking piece
Block the checking piece (if being checked by a rook, bishop or queen)

To help with the second and third points, I calculate a capture mask and a push mask bit-board which represent the set of squares a piece can capture on, and the set of squares a piece can move to respectively. If not in check, then these two masks are both the set of all squares — since we can move anywhere.

However, if we’re in check the capture mask is restricted to the piece giving check as the only valid capture is the one that will get us out of check. If we’re being checked by a piece that can be blocked (rook, bishop or queen), then the push mask is limited to squares between the king and the piece giving check:

let mut capture_mask = Bitboard(0xFFFFFFFFFFFFFFFFu64); // all squares
let mut push_mask    = Bitboard(0xFFFFFFFFFFFFFFFFu64); // all squares

if num_checkers == 1 {
    // if ony one checker, we can evade check by capturing it
    capture_mask = checkers;

    // If the piece giving check is a slider, we can evade check by blocking it
    let checker_square = checkers.bitscan_forward();
    if board.at(checker_square).is_slider() {
        push_mask = opponent_slider_rays_to_square(king_square, board);
    } else {
        // if the piece is not a slider, we can only evade check by capturing
        push_mask = Bitboard(0); // empty bitboard
    }
}

Here’s an example:

The black king is checked by the rook on e5. Since we’re in check from a single piece, we calculate the capture mask as the piece giving check, denoted by red X’s. When calculating captures for black’s knight on g6 we will filter them using this capture mask so that the only valid capture is taking white’s rook. Because we’re in check from a sliding piece, we can also evade check by blocking the attack. We calculate the push mask as the set of squares between the checker and the king, denoted by green X’s. Filtering knight pushes (i.e. non-captures) using this mask reveals that the only valid knight push is to block the check by moving to e7.

Gotcha: En-passant check evasions

You might be wondering why it’s worth calculating separate push masks and capture masks — why not just use one mask to filter all types of move?

The reason has to do with evading check using en-passant captures. En-passant captures are unique in chess because the piece being captured is not on the square the capturing piece moves to.

Look at the following example: 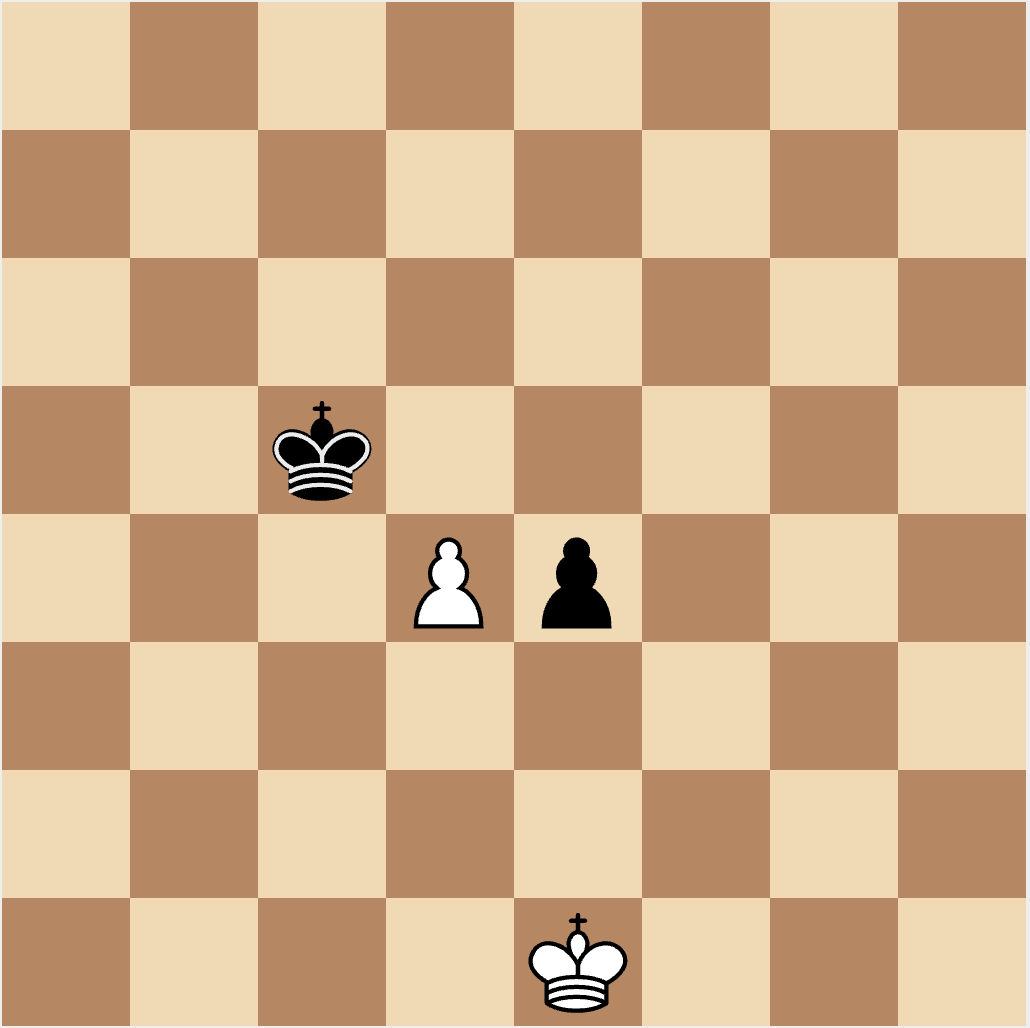Here black is in check due to white’s pawn on d4. Our capture mask should include d4 so we can take the pawn with our pawn on e4 using en-passant, evading the check.

Here’s another example: 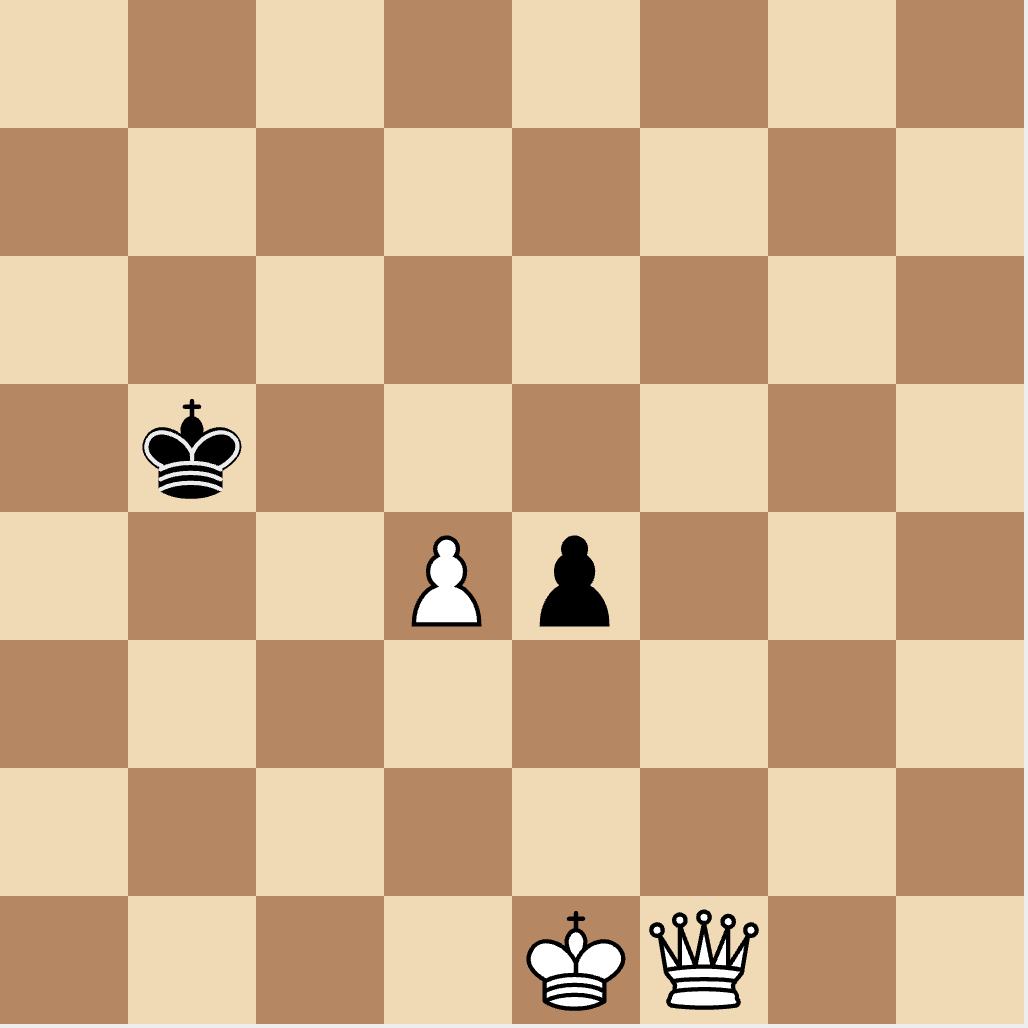Here black is in check from white’s queen on f1. Since our push mask should include all the squares between black’s king and white’s queen, we can also use an en-passant to block this check. En-passant pushes black’s pawn to d3 blocking the check from white’s queen.

The difference between the two is that the capture mask represents a piece you need to remove — since it’s giving check. The push mask represents squares you need to move to — to block a check.

Part 3: Pinned pieces

Whether in check or not, you’ll need to calculate pinned pieces. In chess a pin (to be technical, an absolute pin, as there are other kinds of pins), is when a piece is “pinned” to your king by a sliding enemy piece — if you move it you’ll be in check. Here black’s rook on e6 is pinned to the e-file. It can’t move left or right because doing so would leave black in check from white’s queen on e3.

Moves for pinned pieces

When a piece is pinned, it can only move towards or away from the pinner, it can’t leave the line between the attacking piece and the king.

For the example here black’s rook can only move to the squares denoted by a red X:

Finding the ‘pin rays’ between the king and a pinner can be an expensive calculation. In my engine I do this by first finding all the pinned pieces. This is done by calculating (for each possible direction):

Moves from the opponent’s sliding pieces.
“Sliding piece” moves from my king in the opposite direction.
The overlap of these two rays.

If the result of 3) lands on one of my pieces, then it is pinned.

Once all the pinned pieces are identified, you can remove them from the board and calculate the moves from the enemy’s pinning piece to your king. This will give you a “ray” of legal moves for each of your pinned pieces.

Note that since knights can only move in an L-shape, they can never move along a pin ray. The only piece types you need to consider are:

On a diagonal ray: bishops, queens, and pawns (captures only).
On a non-diagonal ray: rooks, queens, and pawns (pushes only).

Part 4: Other moves

At this point we have calculated all the legal king moves, and all the legal moves for pinned pieces. By making a bit-board of pinned pieces, we can filter them out from the rest of the move generation. Calculating the moves for all remaining pieces can be done as normal, making sure to use the capture mask and push mask to filter moves if there is a check.

You can’t castle if you’re in check so we can skip this if num_checkers is not zero.

Gotcha: En-passant discovered check

There is one remaining gotcha when calculating legal moves. If you’re writing a move generator and hitting your head against a hard-to-find bug, it’s probably this one!

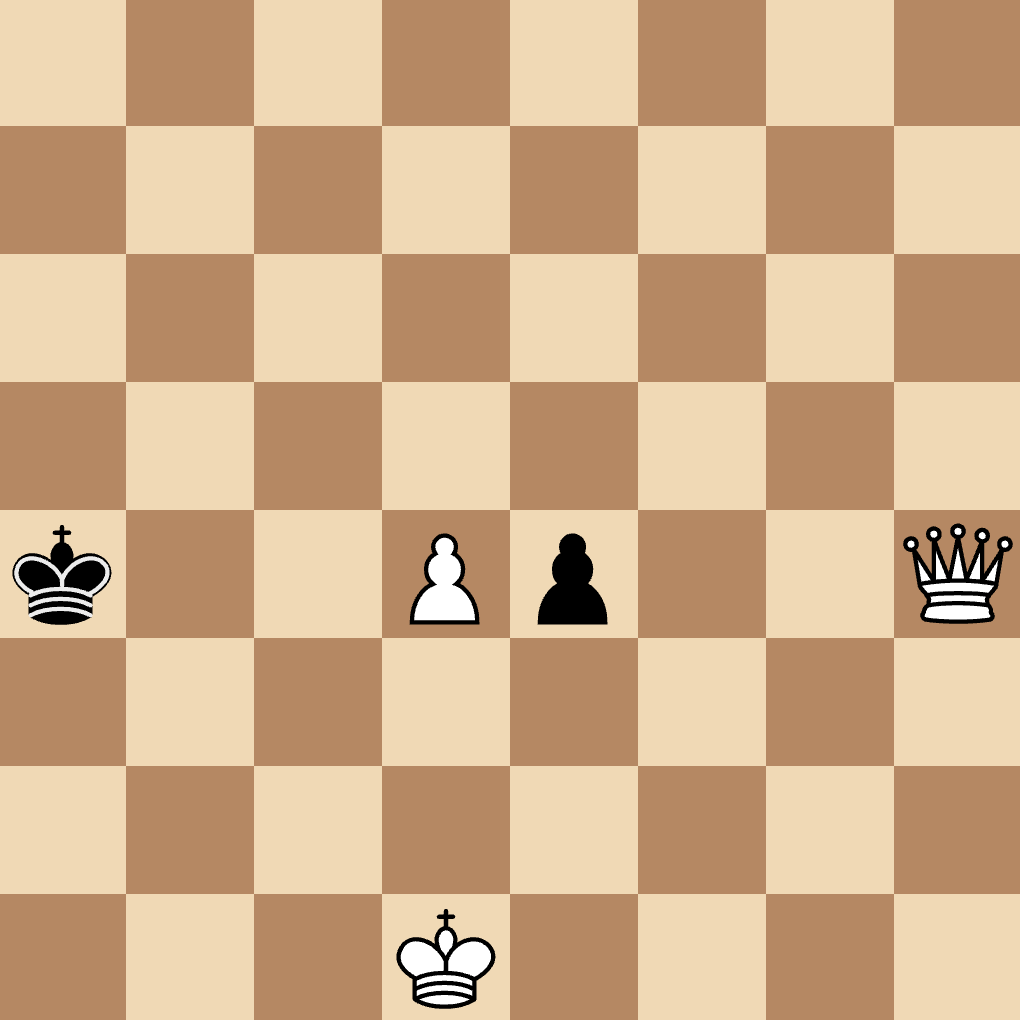
Here black may try to take white’s pawn on e4 en-passant. However this leaves rank-4 entirely open exposing discovered check. Since there are two blocking pieces, this is something that the pin-generation phase does not pick up.

In my engine I deal with this by checking for this kind of attack each time I generate an en-passant move. Since en-passant moves are very rare, this adds very little overhead to the move generation function. It removes the moving pawn and the captured pawn from the board and checks if there is an attack from the king in a horizontal direction to an enemy rook or queen. If there is, then it’s an invalid en-passant capture.

Testing

Move generating functions need rigorous testing to avoid subtle edge-case bugs. One way to test move generation is using ‘ perft ’ positions. A perft (performance test) function tells you the number of nodes at a given depth for a given position. For example, for the starting chess position there are 119,060,324 nodes six layers deep.

By building a perft function and comparing your the results to ‘correct’ chess engines, you can be confident in the accuracy of your move generation.

I used the these test positions from a variety of sources as well as some I discovered while debugging.

Performance

Since chess has a high branching factor of about 35-38 moves per position, a good position evaluator is more valuable than a fast move generator. Although fast move generator can try more potential moves, a good position evaluation can help you prune huge chunks off the search tree, massively reducing the number of positions you need to search.

Qperft is a purpose-built perft calculator by H.G.Muller. It’s considered one of the fastest move generators out there so my goal with my engine was to take at most twice as long as qperft.

Compiled with gcc -O3, qperft hits a staggering 190 million nodes per second for the starting position (single-threaded, with hashing disabled) on my MacBook Pro. By comparison, I recently hit 106 million nodes per second with my engine for the same position (also single-threaded, with hashing disabled).

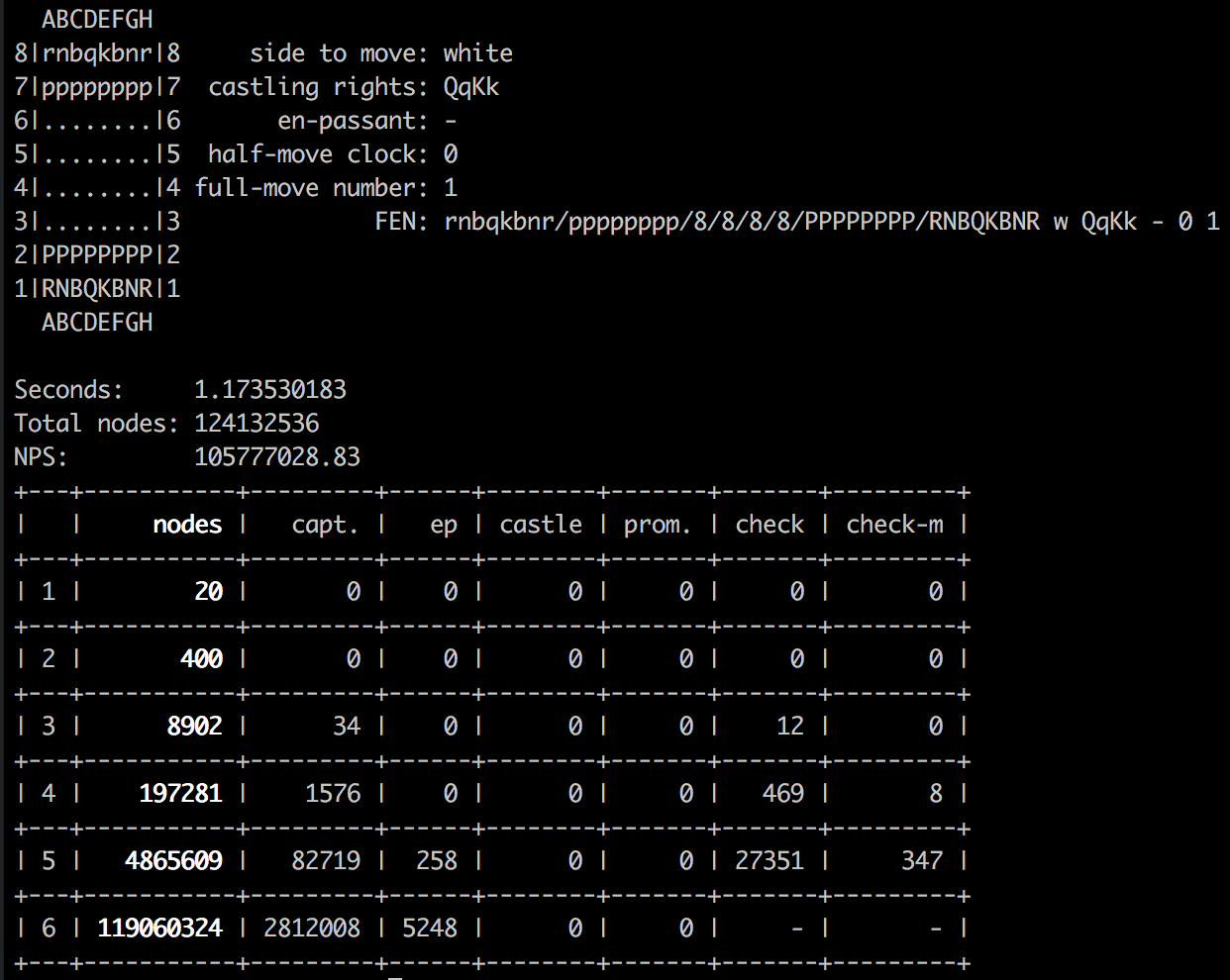
100 million NPS is not great, but is “good enough” for now. Initially I started at 40 million NPS, and increased it by:

Using SIMD instructions to do bit-wise operations on multiple bit-boards at the same time.
Using Kogge-Stone Generators when calculating slider moves for multiple pieces at the same time (e.g. calculating king danger squares or pin rays).
Using the o^(o-2r) trick when calculating moves for individual sliding pieces, using the intel PSHUFB instruction to do byte-swaps on 128-bit registers to calculate diagonal attacks.
Using the OSX profiling tool Instruments (which works great with Rust by the way), to identify slow areas of code.

Weirdly, other positions get much closer to Qperft’s performance — for example, r3k2r/Pppp1ppp/1b3nbN/nP6/BBP1P3/q4N2/Pp1P2PP/R2Q1RK1 w kq - 0 1 gets within 90% of qperft’s NPS at depth 6.

With this I’ve ‘finished’ move generation, and move onto the next part… evaluation.

PS. check out Lichess.org’s board editor if you want super-simple chess diagrams.