Fantasy Machine Learning
As we all know, machine learning is the Hot New Thing™ in tech. Fantasy football is an online game a lot of my friends play. I know as much about machine learning as I do about fantasy football (which is to say, not a lot). So since I’m stuck in a hotel in the middle of a freezing cold Ontarian winter it seemed like a good idea to try and mix the two.
Fantasy Football
Fantasy Premier League is one of the most popular online games in the UK, boasting over five million players. You choose a team of footballers from the UK Premier League and each week your team is assigned points based on how they perform in their real-world matches. The goal is to create the team that wins the most points. You pick your initial team from a budget of £100M, and can transfer a limited number of team-members each week, their price fluctuating based on their popularity with fellow players.
Here’s a list of things a player can do to earn or lose points for your team:
| Action | Points |
|---|---|
| Playing up to 60 minutes | 1 |
| Playing 60 minutes or more (excluding injury time) | 2 |
| Goal scored by a goalkeeper or defender | 6 |
| Goal scored by a midfielder | 5 |
| Goal scored by a forward | 4 |
| Goal assist | 3 |
| Clean sheet by a goalkeeper or defender | 4 |
| Clean sheet by a midfielder | 1 |
| Every 3 saves by a goalkeeper | 1 |
| Penalty save | 5 |
| Penalty miss | -2 |
| Being among the best players in a match | 1-3 |
| Every 2 goals conceded by a goalkeeper or defender | -1 |
| Yellow card | -1 |
| Red card | -3 |
| Own goal | -2 |
Let’s grab some data and see what we can find. If you sign-up for a Fantasy Premier League account, go to the create team page and inspect your network requests, you’ll see a lovely blob of json containing (among other things) statistics about the 625 players in the league. Once I converted this to CSV and uploaded it to Google Cloud Storage I was able to import it into Google Cloud Datalab, a python-based machine learning workbench.
import pandas as pd
from io import BytesIO
%gcs read \
--object "gs://fantasy_premier_league/2018-02-06.csv" \
--variable raw
# element_type is a value from 1 to 4 representing position
# convert this into binary values for each position, as well as a 'position' string
df['keeper'] = df['element_type'].map(lambda x: 1 if x == 1 else 0)
df['defender'] = df['element_type'].map(lambda x: 1 if x == 2 else 0)
df['midfielder'] = df['element_type'].map(lambda x: 1 if x == 3 else 0)
df['forward'] = df['element_type'].map(lambda x: 1 if x == 4 else 0)
df['position'] = df['element_type'].map(lambda x: ['keeper', 'defender', 'midfielder', 'forward'][x-1])
df[['web_name', 'position', 'now_cost', 'total_points']] \
.sort_values(by=['total_points'], ascending=False) \
.head(10)
(costs in are units of £0.1M)
Looks like Liverpool’s Mohamed Salah is winning by a decent margin. However at £10.3M, he’s one of the most expensive players available. Let’s plot costs versus total points to see if there’s a relation (hover over the points to see the player names):
It looks like there is only a weak correlation between cost and points. This means there should be plenty of opportunities to find players that provide good value for money. Let’s see who achieved the most points per £100k in costs:
df['points_per_100k'] = df['total_points'] / df['now_cost']
df.loc[np.isfinite(df['points_per_100k'])] \
[['web_name', 'now_cost', 'total_points', 'points_per_100k']] \
.sort_values(by=['points_per_100k'], ascending=False) \
.head(10)
And the winner is Burnley’s keeper Nick Pope with 113 points at a cost of just £4.9M. Given the number of goalkeepers in the list, it looks like they might be undervalued by the community.
Now that we have some idea about the data, lets see if we can pick a team.
Linear Programming
Linear programming (LP, also called linear optimization) is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming (mathematical optimization). [Wikipedia]
Linear programming is kind of like simultaneous equations extended to more dimensions. An example might be if you’re a farmer and you need to decide how much land to allocate to cows and how much to allocate to corn. Corn makes $1000/acre and takes up 2 days’ work per acre. Cows make $5000/acre but takes up 20 days’ work. You can only work 365 days, and you only have 50 acres — how much of each should you grow?
Profit = 1000 * corn + 5000 * cows
Time = 2 * corn + 20 * cows
Land Used = corn + cows
We can solve this using Scikit’s Linprog method. By expressing the above constraints as matrices and passing them to lingprog, we can let Scikit do the hard work for us. Note that since linprog tries to minimize whatever you pass it, we have to make the profit negative when we pass it in so it tries to maximizes it.
profit = [
1000, # profit for corn per acre
5000 # profit for cows per acre
]
params = [
[2, 20], # number of days per acre for corn and cows
[1, 1] # amount of land used per acre for corn and cows
]
upper_bounds = [
365, # max total number of days (1 year)
50 # max total amount of land
]
from scipy.optimize import linprog
results = linprog(
-profit, # negative profit so linprog will maximize, not minimize
params,
upper_bounds
).x
corn = results[0]
cows = results[1]
print("%.2f acres of corn" % cows)
print("%.2f acres of cows" % corn)
print("total profit $%.2f" % (corn * profit[0] + cows * profit[1] )
print("total days %.2f" % (corn * params[0][0] + cows * params[0][1] ))
print("total land %.2f" % (corn * params[1][0] + cows * params[1][1] ))
14.72 acres of corn
35.28 acres of cows
total profit $108888.89
total days 365.00
total land 50.00
Boom! so the farmer can make $109k. Under the hood Scikit uses the Simplex algorithm which I think I probably learnt at university and immediately forgot. In any case, it’s fast and it works.
Linear Teams
Let’s try and express fantasy football as a set of linear programming constraints! As well as having a budget of £100M and a maximum of 15 players, you can only have certain numbers of players for each position: 2 keepers, 5 defenders, 5 midfielders and 3 forwards. Let’s use linprog to try and make a team using these constraints:
# costs is an array with the cost of each player
costs = df['now_cost']
# keepers is an array with a 1 if a player increases the number of keepers or 0 otherwise
keepers = df['keeper']
# defenders is an array with a 1 if a player increases the number of defenders or 0 otherwise
defenders = df['defender']
# midfielders is an array with a 1 if a player increases the number of midfielders or 0 otherwise
midfielders = df['midfielder']
# forwards is an array with a 1 if a player increases the number of forwards or 0 otherwise
forwards = df['forward']
# players is an array with a 1 if a player increases the number of players or 0 otherwise
# ie, all ones
players = np.ones(len(df))
params = np.array([
costs,
keepers,
defenders,
midfielders,
forwards,
players,
])
upper_bounds = np.array([
1000, # max cost
2, # max keepers
5, # max defenders
5, # max midfielders
3, # max fowards
15, # max players
])
# total_points is an array of total points per player
# this is what we want to maximize
total_points = df['total_points']
from scipy.optimize import linprog
df['selected'] = linprog(
-total_points, # negative profit so linprog will maximize, not minimize
params,
upper_bounds
).x
print("cost: %.2f" % (df['now_cost'] * df['selected']).sum())
print("keepers: %.2f" % (df['keeper'] * df['selected']).sum())
print("defenders: %.2f" % (df['defender'] * df['selected']).sum())
print("midfielders: %.2f" % (df['midfielder'] * df['selected']).sum())
print("forwards: %.2f" % (df['forward'] * df['selected']).sum())
print("players: %.2f" % (df['selected']).sum())
print("points: %.2f" % (df['selected'] * df['total_points']).sum())
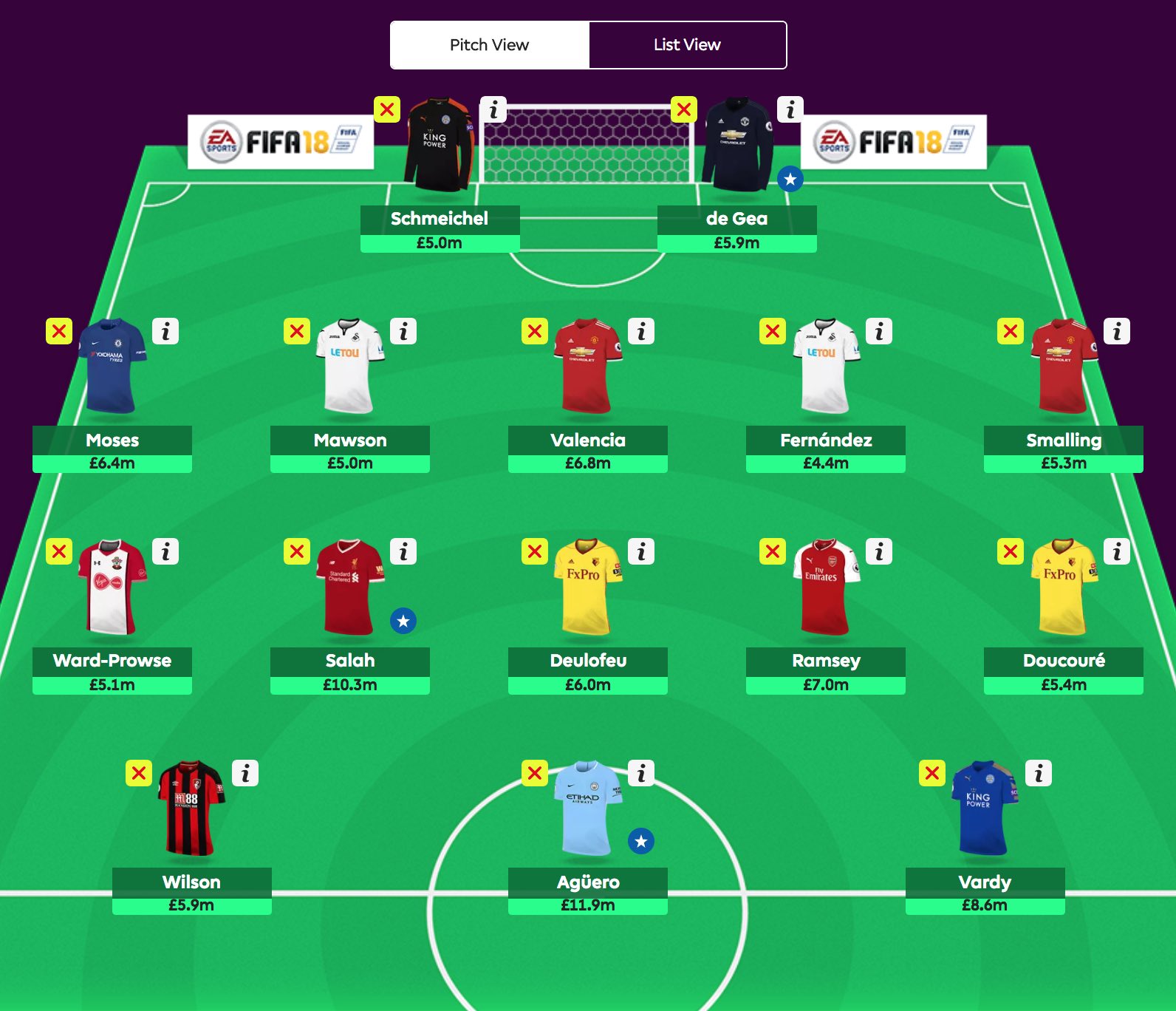
df.loc[df['selected'] != 0] \
[['web_name', 'position', 'now_cost', 'total_points', 'points_per_100k', 'selected']] \
.sort_values(by=['points_per_100k'], ascending=False)
cost: 1000.00
keepers: 2.00
defenders: 5.00
midfielders: 5.00
forwards: 0.00
players: 12.00
points: 1975.06
Linprog has done exactly what we asked for and not at all what we wanted. It managed to spend exactly £100M, and managed to find a set of players who made a total of 1975 points. However in doing so it decided to buy 5 copies of Salah and 4.8 Alonsos which breaks not only the rules of fantasy football but also the rules of nature.
Fortunately linprog allow you to specify bounds on the solution so we can ensure we chose no more than 1 of each player and no fewer than 0:
bounds = [(0, 1) for x in range(len(df))]
df['selected'] = linprog(
-total_points, # negative profit so linprog will maximize, not minimize
params,
upper_bounds,
bounds=bounds
).x
cost: 1000.00
keepers: 2.00
defenders: 5.00
midfielders: 5.00
forwards: 3.00
players: 15.00
points: 1849.00
This is much better, we are able to field complete players, have spent 100% of the budget, and have 1849 of “points experience” available. Note there is an optimisation in that not all our players can produce points at the same time as 4 must be “on the bench” each week. In practise this acts as a safety net since the rules state that if one of your starting players doesn’t play, he is substituted by a player on the bench who plays the same position.
Another big assumption I’ve made is that a player’s points this season is a good estimator of points in the next match. This is where you’d want to crack open further machine learning algorithms like linear regression or neural networks to make a better prediction of points earned in the next match based on more features.
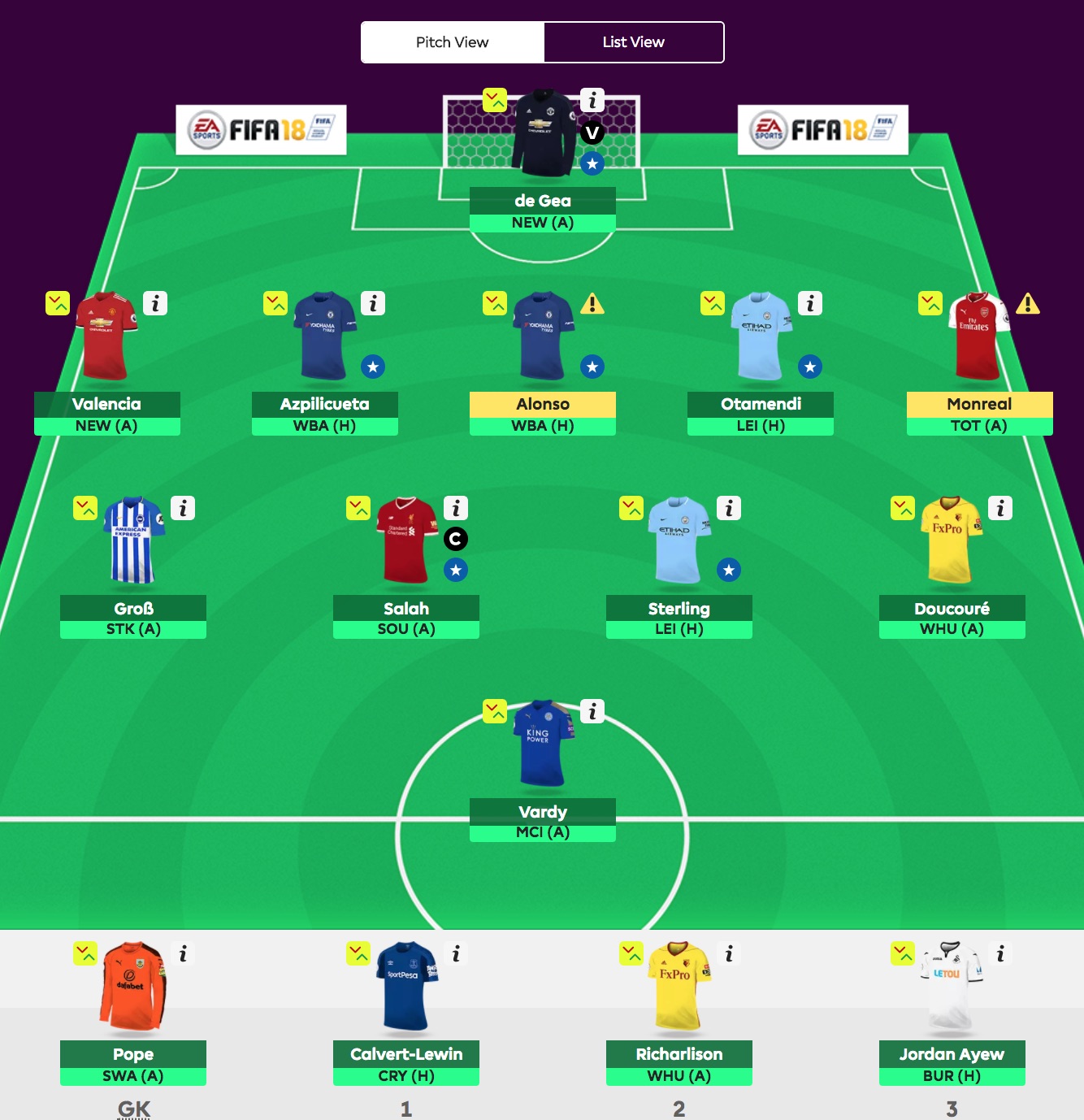
Anyway, please allow me to introduce the Ottawa Pythons: